
Therefore, it is proved that the derivative of logarithm of a function with respect to variable is equal to the product of the reciprocal of the function and the derivative of the function. If you have any other trick or big point that I may have missed, leave me a comment below, and we can discuss it.The derivative of logarithmic function can be derived in differential calculus from first principle. This question always comes up, and on this page we do a pretty good job of clearing all doubts.Īnd I think that sums up the essential techniques for solving derivatives.

#How to take derivative of log how to
These formulas are pretty hard to memorize, so it is good to know how to prove them to yourself. Here we learn about the derivative of arcsin(x), arccos(x) and others. To learn about the derivative of the natural log go to this page: Derivative of ln(x). We add another formula to our list using, once again, the definition of the derivative. To learn about the derivative of exponential functions, go to this page. We add another function to the list of those we know how to take the derivative of. To learn about derivatives of trigonometric functions go to this page: Derivatives of Trigonometric Functions. With these in your toolkit you can solve derivatives involving trigonometric functions using other tools like the chain rule or the product rule.

We first need to find those two derivatives using the definition. Two basic ones are the derivatives of the trigonometric functions sin(x) and cos(x). To start building our knowledge of derivatives we need some formulas. The Essential Formulas Derivative of Trigonometric Functions To learn about implicit differentiation go to this page: Implicit Differentiation. Implicit differentiation allows you to find derivatives of functions expressed in a funny way, that we call implicit. The key is in understanding the chain rule. To learn about this method go to this page: The Quotient Rule. b) when x is less than 1 and becomes smaller. That derivative approaches 0, that is, becomes smaller. a) when x is greater than 1 and becomes larger. Differentiate both sides using implicit differentiation. To find the derivative of other logarithmic functions, you must use the change of base formula: loga(x) ln(x)/ln(a). ln y ln x x ln y x ln x ln y ln x x ln y x ln x. First take the logarithm of both sides as we did in the first example and use the logarithm properties to simplify things a little. I'll show you a method for solving derivatives of quotients using the product rule. According to the rule for changing from base e to a different base a: Topic 20 of Precalculus. With logarithmic differentiation we can do this however. The quotient rule is just an special case of the product rule, so you don't need to memorize another formula. To learn about the product rule go to this page: The Product Rule. It is a very useful technique, and one of the few formulas you should memorize in calculus. The product rule allows you to find derivatives of functions that are products of other functions. To learn about the chain rule go to this page: The Chain Rule. With it you'll be able to find the derivative of almost any function.
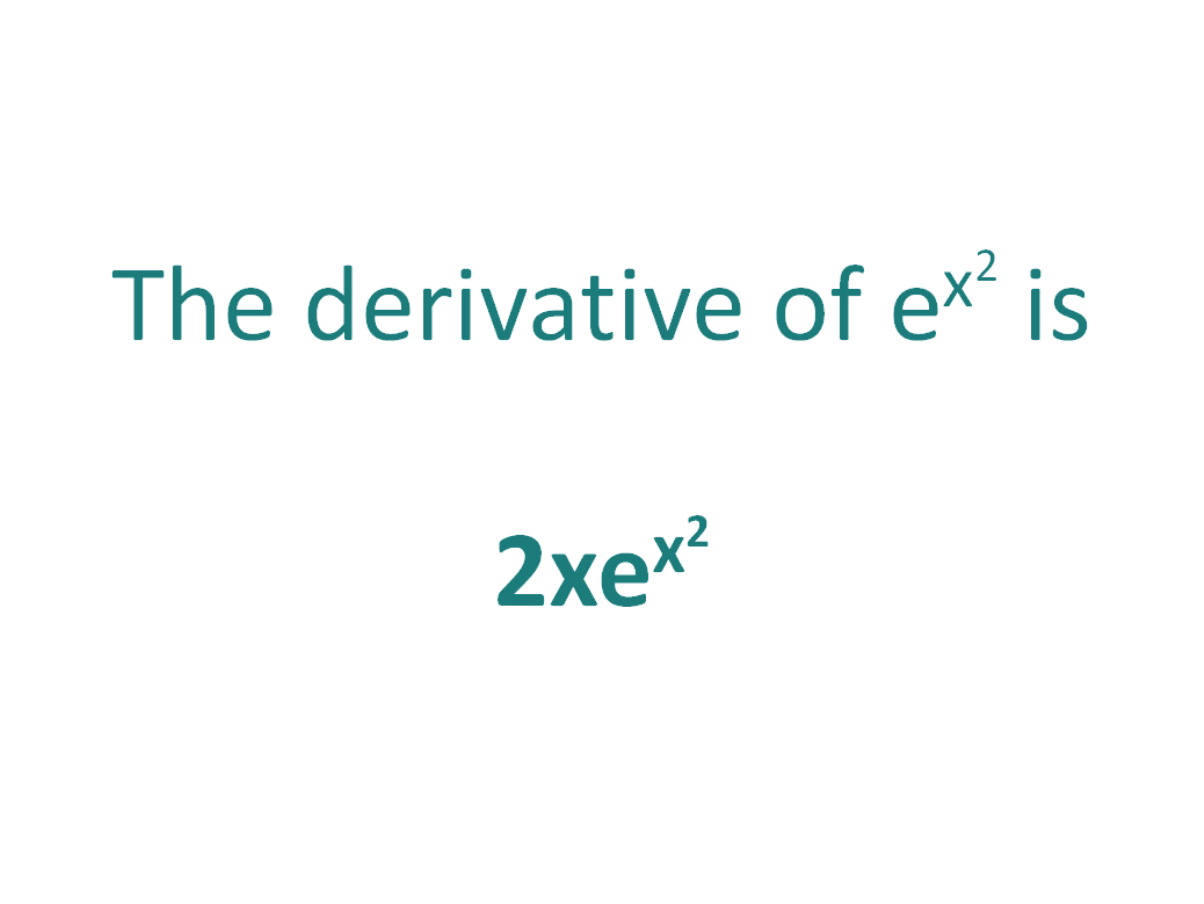
The chain rule is the most important rule for taking derivatives. We talk at length about how to use the definition on the page calculating the derivative by definition. To calculate derivatives this way is a skill.Īs with any skill, you only improve with practice. The most basic way of calculating derivatives is using the definition. This page can be used as a map that can guide you in your study of derivatives, or you can use it to review all the techniques for solving derivatives.Īre you ready? Let's go. I put the techniques you need to learn in an order that would make it easier for you to understand them. Example: Let's take the example when x 2. The expression for the derivative is the same as the expression that we started with that is, e x (d(ex))/(dx)ex What does this mean It means the slope is the same as the function value (the y-value) for all points on the graph. My goal with this page is to make you a derivative solving machine :-). The derivative of e x is quite remarkable. In this page you'll find everything you need to know about solving derivatives.


 0 kommentar(er)
0 kommentar(er)
